IEEE 754浮點數標準詳解
IEEE 754浮點數標準詳解
http://c.biancheng.net/view/314.html
在計算機系統的發展過程中,業界曾經提出過許多種實數的表達方法,比較典型的有相對于浮點數(Floating Point Number)的定點數(Fixed Point Number)。在定點數表達法中,其小數點固定地位于實數所有數字中間的某個位置。例如,貨幣的表達就可以采用這種表達方式,如 55.00 或者 00.55 可以用于表達具有 4 位精度,小數點后有兩位的貨幣值。由于小數點位置固定,所以可以直接用 4 位數值來表達相應的數值。
但我們不難發現,定點數表達法的缺點就在于其形式過于僵硬,固定的小數點位置決定了固定位數的整數部分和小數部分,不利于同時表達特別大的數或者特別小的數。因此,最終絕大多數現代的計算機系統都采納了所謂的浮點數表達法。
浮點數表達法采用了科學計數法來表達實數,即用一個有效數字。一個基數(Base)、一個指數(Exponent)以及一個表示正負的符號來表達實數。比如,666.66 用十進制科學計數法可以表達為 6.6666×102(其中,6.6666 為有效數字,10 為基數,2 為指數)。浮點數利用指數達到了浮動小數點的效果,從而可以靈活地表達更大范圍的實數。
當然,對實數的浮點表示僅作如上的規定是不夠的,因為同一實數的浮點表示還不是唯一的。例如,上面例子中的 666.66 可以表達為 0.66666×103、6.6666×102 或者 66.666×101 三種方式。因為這種表達的多樣性,因此有必要對其加以規范化以達到統一表達的目標。規范的浮點數表達方式具有如下形式:
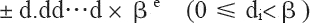
其中,d.dd…d 為有效數字,β 為基數,e 為指數。
有效數字中數字的個數稱為精度,我們可以用 p 來表示,即可稱為 p 位有效數字精度。每個數字 d 介于 0 和基數 β 之間,包括 0。更精確地說,±d0.d1d2…dp-1×βe 表示以下數:
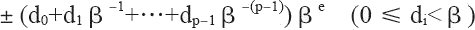
其中,對十進制的浮點數,即基數 β 等于 10 的浮點數而言,上面的表達式非常容易理解。如 12.34,我們可以根據上面的表達式表達為:1×101+2×100+3×10-1+4×10-2,其規范浮點數表達為1.234×101。
但對二進制來說,上面的表達式同樣可以簡單地表達。唯一不同之處在于:二進制的 β 等于 2,而每個數字 d 只能在 0 和 1 之間取值。如二進制數 1001.101,我們可以根據上面的表達式表達為:1×23+0×22+0×21+1×20+1×2-1+0×2-2+1×2-3,其規范浮點數表達為 1.001101×23。
現在,我們就可以這樣簡單地把二進制轉換為十進制,如二進制數 1001.101 轉換成十進制為:
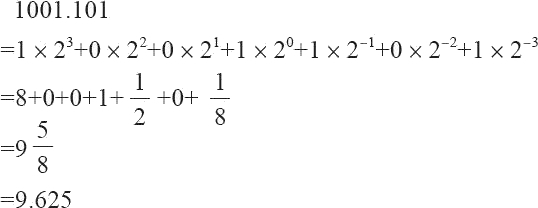
由上面的等式,我們可以得出:向左移動二進制小數點一位相當于這個數除以 2,而向右移動二進制小數點一位相當于這個數乘以 2。如 101.11=3/4,而 10.111=7/8。除此之外,我們還可以得到這樣一個基本規律:一個十進制小數要能用浮點數精確地表示,最后一位必須是 5(當然這是必要條件,并非充分條件)。規律推演如下面的示例所示:

- #include
- int main(void)
- {
- float f1=34.6;
- float f2=34.5;
- float f3=34.0;
- printf("34.6-34.0=%f\n",f1-f3);
- printf("34.5-34.0=%f\n",f2-f3);
- return 0;
- }
34.6-34.0=0.599998
34.5-34.0=0.500000
之所以“34.6-34.0=0.599998”,產生這個誤差的原因是 34.6 無法精確地表達為相應的浮點數,而只能保存為經過舍入的近似值。而這個近似值與 34.0 之間的運算自然無法產生精確的結果。
上面闡述了二進制數轉換十進制數,如果你要將十進制數轉換成二進制數,則需要把整數部分和小數部分分別轉換。其中,整數部分除以 2,取余數;小數部分乘以 2,取整數位。如將 13.125 轉換成二進制數如下:
1、首先轉換整數部分(13),除以 2,取余數,所得結果為 1101。
2、其次轉換小數部分(0.125),乘以 2,取整數位。轉換過程如下:
0.125×2=0.25 取整數位0
0.25×2=0.5 取整數位0
0.5×2=1 取整數位1
除此之外,與浮點表示法相關聯的其他兩個參數是“最大允許指數”和“最小允許指數”,即 emax 和 emin。由于存在 βp 個可能的有效數字,以及 emax-emin+1 個可能的指數,因此浮點數可以按 [log2(emax-emin+1)]+[log2(βp)]+1 位編碼,其中最后的 +1 用于符號位。
浮點數表示法
直到 20 世紀 80 年代(即在沒有制定 IEEE 754 標準之前),業界還沒有一個統一的浮點數標準。相反,很多計算機制造商根據自己的需要來設計自己的浮點數表示規則,以及浮點數的執行運算細節。另外,他們常常并不太關注運算的精確性,而把實現的速度和簡易性看得比數字的精確性更重要,而這就給代碼的可移植性造成了重大的障礙。直到 1976 年,Intel 公司打算為其 8086 微處理器引進一種浮點數協處理器時,意識到作為芯片設計者的電子工程師和固體物理學家也許并不能通過數值分析來選擇最合理的浮點數二進制格式。于是,他們邀請加州大學伯克利分校的 William Kahan 教授(當時最優秀的數值分析家)來為 8087 浮點處理器(FPU)設計浮點數格式。而這時,William Kahan 教授又找來兩個專家協助他,于是就有了 KCS 組合(Kahn、Coonan和Stone),并共同完成了 Intel 公司的浮點數格式設計。
由于 Intel 公司的 KCS 浮點數格式完成得如此出色,以致 IEEE(Institute of Electrical and Electronics Engineers,電子電氣工程師協會)決定采用一個非常接近 KCS 的方案作為 IEEE 的標準浮點格式。于是,IEEE 于 1985 年制訂了二進制浮點運算標準 IEEE 754(IEEE Standard for Binary Floating-Point Arithmetic,ANSI/IEEE Std 754-1985),該標準限定指數的底為 2,并于同年被美國引用為 ANSI 標準。目前,幾乎所有的計算機都支持 IEEE 754 標準,它大大地改善了科學應用程序的可移植性。
考慮到 IBM System/370 的影響,IEEE 于 1987 年推出了與底數無關的二進制浮點運算標準 IEEE 854,并于同年被美國引用為 ANSI 標準。1989 年,國際標準組織 IEC 批準 IEEE 754/854 為國際標準 IEC 559:1989。后來經修訂后,標準號改為 IEC 60559。現在,幾乎所有的浮點處理器完全或基本支持 IEC 60559。同時,C99 的浮點運算也支持 IEC 60559。
IEEE 浮點數標準是從邏輯上用三元組{S,E,M}來表示一個數 V 的,即 V=(-1)S×M×2E,如圖1 所示。

圖 1
其中:符號位 s(Sign)決定數是正數(s=0)還是負數(s=1),而對于數值 0 的符號位解釋則作為特殊情況處理。
有效數字位 M(Significand)是二進制小數,它的取值范圍為 1~2-ε,或者為 0~1-ε。它也被稱為尾數位(Mantissa)、系數位(Coefficient),甚至還被稱作“小數”。
指數位 E(Exponent)是 2 的冪(可能是負數),它的作用是對浮點數加權。
浮點數格式是一種數據結構,它規定了構成浮點數的各個字段、這些字段的布局及算術解釋。IEEE 754 浮點數的數據位被劃分為三個段,從而對以上這些值進行編碼。其中,一個單獨的符號位 s 直接編碼符號 s;k 位的指數段 exp=ek-1…e1e0,編碼指數 E;n 位的小數段 frac=fn-1…f1f0,編碼有效數字 M,但是被編碼的值也依賴于指數域的值是否等于 0。
根據 exp 的值,被編碼的值可以分為如下幾種不同的情況。
1) 格式化值
當指數段 exp 的位模式既不全為 0(即數值 0),也不全為 1(即單精度數值為 255,以單精度數為例, 8 位的指數為可以表達 0~255 的 255 個指數值;雙精度數值為 2047)的時候,就屬于這類情況。如圖 2 所示。

圖 2
我們知道,指數可以為正數,也可以為負數。為了處理負指數的情況,實際的指數值按要求需要加上一個偏置(Bias)值作為保存在指數段中的值。因此,這種情況下的指數段被解釋為以偏置形式表示的有符號整數。即指數的值為:E=e-Bias
其中,e 是無符號數,其位表示為 ek-1…e1e0,而 Bias 是一個等于 2k-1-1(單精度是 127,雙精度是 1023)的偏置值。由此產生指數的取值范圍是:單精度為 -126~+127,雙精度為 -1022~+1023。
對小數段 frac,可解釋為描述小數值 f,其中 0≤f<1,其二進制表示為 0.fn-1…f1f0,也就是二進制小數點在最高有效位的左邊。有效數字定義為 M=1+f。有時候,這種方式也叫作隱含的以 1 開頭的表示法,因為我們可以把 M 看成一個二進制表達式為 1.fn-1fn-2…f0 的數字。既然我們總是能夠調整指數 E,使得有效數字 M 的范圍為 1≤M<2(假設沒有溢出),那么這種表示方法是一種輕松獲得一個額外精度位的技巧。同時,由于第一位總是等于 1,因此我們就不需要顯式地表示它。拿單精度數為例,按照上面所介紹的知識,實際上可以用 23 位長的有效數字來表達 24 位的有效數字。比如,對單精度數而言,二進制的 1001.101(即十進制的 9.625)可以表達為 1.001101×23,所以實際保存在有效數字位中的值為:
00110100000000000000000
即去掉小數點左側的 1,并用 0 在右側補齊。根據上面所闡述的規則,下面以實數 -9.625 為例,來看看如何將其表達為單精度的浮點數格式。具體轉換步驟如下:
1、首先,需要將 -9.625 用二進制浮點數表達出來,然后變換為相應的浮點數格式。即 -9.625 的二進制為 1001.101,用規范的浮點數表達應為 1.001101×23。
2、其次,因為 -9.625 是負數,所以符號段為 1。而這里的指數為 3,所以指數段為 3+127=130,即二進制的 10000010。有效數字省略掉小數點左側的 1 之后為 001101,然后在右側用零補齊。因此所得的最終結果為:
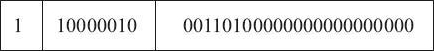
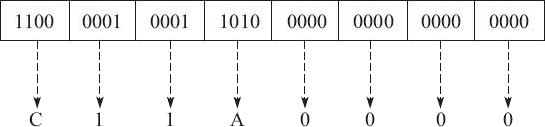
即最終的十六進制結果為 0xC11A0000。
2) 特殊數值
IEEE 標準指定了以下特殊值:±0、反向規格化的數、±∞ 和 NaN(如下表所示)。這些特殊值都是使用 emax+1 或 emin-1 的指數進行編碼的。


圖 3
一般情況下,我們將 0/0 或:
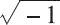
視為導致計算終止的不可恢復錯誤。但是,一些示例表明在這樣的情況下繼續進行計算是有意義的。這時候就可以通過引入特殊值 NaN,并指定諸如 0/0 或
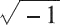
之類的表達式計算來生成 NaN 而不是停止計算,從而避免此問題。下表中列出了一些可以導致 NaN 的情況。

無窮:當指數段 exp 全為 1,小數段全為 0 時,得到的值表示無窮。當 s=0 時是 +∞,或者當 s=1 時是 -∞。如圖 4 所示。

圖 4
無窮用于表達計算中產生的上溢問題。比如兩個極大的數相乘時,盡管兩個操作數本身可以保存為浮點數,但其結果可能大到無法保存為浮點數,必須進行舍入操作。根據IEEE標準,此時不能將結果舍入為可以保存的最大浮點數(因為這個數可能與實際的結果相差太遠而毫無意義),而應將其舍入為無窮。對于結果為負數的情況也是如此,只不過此時會舍入為負無窮,也就是說符號域為1的無窮。
3) 非格式化值
當指數段 exp 全為 0 時,所表示的數就是非規格化形式,如圖 5 所示。

圖 5
在這種情況下,指數值 E=1-Bias,而有效數字的值 M=f,也就是說它是小數段的值,不包含隱含的開頭的 1。
非規格化值有兩個用途:
第一,它提供了一種表示數值 0 的方法。因為規格化數必須得使有效數字 M 在范圍 1≤M<2 之中,即 M≥1,因此它就不能表示 0。實際上,+0.0 的浮點表示的位模式為全 0(即符號位是 0,指數段全為 0,而小數段也全為 0),這就得到 M=f=0。令人奇怪的是,當符號位為 1,而其他段全為 0 時,就會得到值 -0.0。根據 IEEE 的浮點格式來看,值 +0.0 和 -0.0 在某些方面是不同的。
第二,它表示那些非常接近于 0.0 的數。它們提供了一種屬性,稱為逐漸下溢出。其中,可能的數值分布均勻地接近于 0.0。
下面的單精度浮點數就是一個非格式化的示例。
它被轉換成十進制表示大約等于 1.4×10-45,實際上它就是單精度浮點數所能表達的最小非格式化數。以此類推,格式化值和非格式化值所能表達的非負數值范圍如下表所示。


標準浮點格式
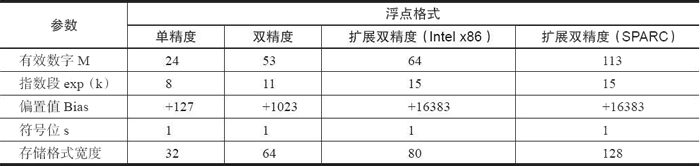
IEEE 754標準準確地定義了單精度和雙精度浮點格式,并為這兩種基本格式分別定義了擴展格式,如下所示:- 單精度浮點格式(32 位)。
- 雙精度浮點格式(64 位)。
- 擴展單精度浮點格式(≥43 位,不常用)。
- 擴展雙精度浮點格式(≥79 位,一般情況下,Intel x86 結構的計算機采用的是 80 位,而 SPARC 結構的計算機采用的是 128 位)。
1) 單精度浮點格式
單精度浮點格式共 32 位,其中,s、exp 和 frac 段分別為 1 位、k=8 位和 n=23 位,如圖 6 所示。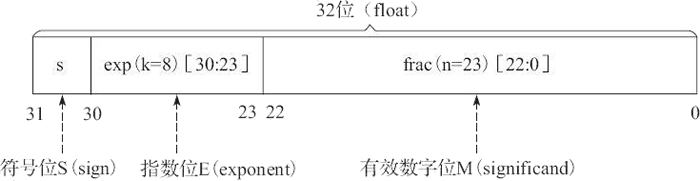
圖 6
其中,32 位中的第 0 位存放小數段 frac 的最低有效位 LSB(least significant bit),第 22 位存放小數段 frac 的最高有效位 MSB(most significant bit);第 23 位存放指數段 exp 的最低有效位 LSB,第 30 位存放指數段 exp 的最高有效位 MSB;最高位,即第 31 位存放符號 s。例如,單精度數 8.25 的存儲方式如圖 7 所示。
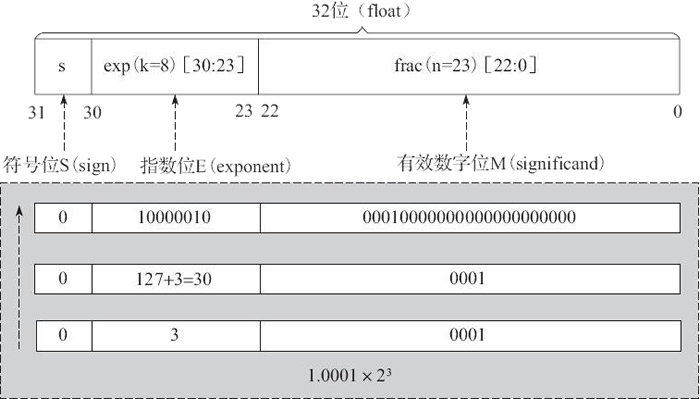
圖 7
2) 雙精度浮點格式
雙精度浮點格式共 64 位,其中,s、exp 和 frac 段分別為 1 位、k=11 位和 n=52 位,如圖 8 所示。
圖 8
其中,frac[31:0] 存放小數段的低 32 位(即第 0 位存放整個小數段的最低有效位 LSB,第 31 位存放小數段低 32 位的最高有效位 MSB);frac[51:32] 存放小數段的高 20 位(即第 32 位存放高 20 位的最低有效位 LSB,第 51 位存放整個小數段的最高有效位 MSB);第 52 位存放指數段 exp 的最低有效位 LSB,第 62 位存放指數段 exp 的最高有效位 MSB;最高位,即第 63 位存放符號 s。
在 Intel x86 結構的計算機中,數據存放采用的是小端法(Little Endian),故較低地址的 32 位的字中存放小數段的 frac[31:0] 位。而在 SPARC 結構的計算機中,因其數據存放采用的是大端法(Big Endian),故較高地址的 32 位字中存放小數段的 frac[31:0] 位。
前面主要討論了 IEEE 754 的單精度與雙精度浮點格式,下表對浮點數的相關參數進行了總結,有興趣的讀者可以根據此表對其他浮點格式進行深入解讀。

舍入誤差
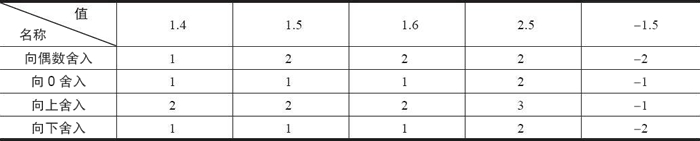
舍入誤差是指運算得到的近似值和精確值之間的差異。大家知道,由于計算機的字長有限,因此在進行數值計算的過程中,對計算得到的中間結果數據要使用相關的舍入規則來取近似值,而這導致計算結果產生誤差。在浮點數的舍入問題上,IEEE 浮點格式定義了 4 種不同的舍入方式,如下表所示。其中,默認的舍入方法是向偶數舍入,而其他三種可用于計算上界和下界。

下表是 4 種舍入方式的應用舉例。這里需要特別說明的是,向偶數舍入(向最接近的值舍入)方式會試圖找到一個最接近的匹配值。因此,它將 1.4 舍入成 1,將 1.6 舍入成 2,而將 1.5 和 2.5 都舍入成 2。
或許看了上面的內容你會問:為什么要采用向偶數舍入這樣的舍入策略,而不直接使用我們已經習慣的“四舍五入”呢?
其原因我們可以這樣來理解:在進行舍入的時候,最后一位數字從 1 到 9,舍去的有 1、2、3、4;它正好可以和進位的 9、8、7、6 相對應,而 5 卻被單獨留下。如果我們采用四舍五入每次都將 5 進位的話,在進行一些大量數據的統計時,就會累積比較大的偏差。而如果采用向偶數舍入的策略,在大多數情況下,5 舍去還是進位概率是差不多的,統計時產生的偏差也就相應要小一些。
同樣,針對浮點數據,向偶數舍入方式只需要簡單地考慮最低有效數字是奇數還是偶數即可。例如,假設我們想將十進制數舍入到最接近的百分位。不管用哪種舍入方式,我們都將把 1.2349999 舍入到 1.23,而將 1.2350001 舍入到 1.24,因為它們不是在 1.23 和 1.24 的正中間。另一方面我們將把兩個數 1.2350000 和 1.2450000 都舍入到 1.24,因為 4 是偶數。
由IEEE浮點格式定義的舍入方式可知,不論使用哪種舍入方式,都會產生舍入誤差。如果在一系列運算中的一步或幾步產生了舍入誤差,在某些情況下,這個誤差將會隨著運算次數的增加而積累得很大,最終會得出沒有意義的運算結果。因此,建議不要將浮點數用于精確計算。
當然,理論上增加數字位數可以減少可能會產生的舍入誤差。但是,位數是有限的,在表示無限浮點數時仍然會產生誤差。在用常規方法表示浮點數的情況下,這種誤差是不可避免的,但是可以通過設置警戒位來減小。
除此之外,IEEE 754 還提出 5 種類型的浮點異常,即上溢、下溢、除以零、無效運算和不精確。其中,每類異常都有單獨的狀態標志。鑒于篇幅有限,本節就不再詳細介紹。
關注微信公眾號「站長嚴長生」,在手機上閱讀所有教程,隨時隨地都能學習。本公眾號由C語言中文網站長運營,每日更新,堅持原創,敢說真話,凡事有態度。
分享




